0Lösungsverfahren für quadratische Ungleichungen
x² - 6x +5 0
1. Mit Hilfe der Anschauung:
Der Satz des Vieta oder die Lösungsformel (x1/2 = ...) liefert die Schnittpunkte der
Parabel y= x² - 6x +5 x1 = 5 und x2 = 1 und damit eine Faktorzerlegung in
y= x² - 6x + 5 = (x - 1)*(x - 5)
Die Parabel ist nach oben geöffnet, hat also die folgende Form.
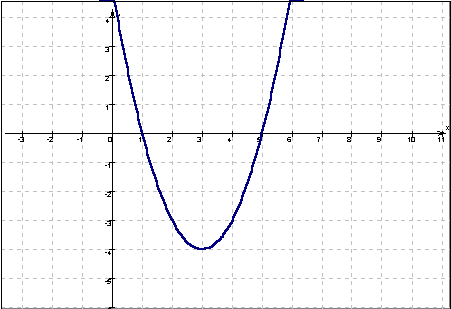
Für welche x-Werte gilt: y= x² -5x+6 0 ? Offensichtlich im Bereich zwischen
1 und 5 also
L = [1;5]. Die entsprechenden y-Werte variieren zwischen 0 und –4.
Für die Bestimmung der Lösungsmenge reicht es aber aus, wenn man die Nullstellen und die Form (nach oben-,nach unten geöffnet) weis.
2. Formale Lösung: Faktorzerlegung durch die Lösungsformel oder den S.v. Vieta in
(x-1)*(x-5) 0
Das Produkt ist negativ, falls einer der beiden Faktoren positiv, der andere
negativ ist. Es gibt also 2 Möglichkeiten:
1: x-1 0 und x-5 
0
x1 und x 5
L1 = {}
2: x-1 0 und x-5 0
x1 und x 5
L1 = [1;5]